GeniePath:自适应感受路径的图神经网络
GeniePath,蚂蚁金服发表于 KDD 2018,一种可扩展的能够学习自适应感受路径的图神经网络框架。定义在具有排列不变性的图数据上(permutation invariant graph data)。其自适应路径层(adaptive path layer)包括两个互补的功能单元,分别用来进行广度与深度的探索,前者用来学习一阶邻域节点的权重,后者用来提取和过滤高阶邻域内汇聚的信息。在直推(transductive)和归纳(inductive)两种学习任务的实验中,均达到了 state-of-the-art 的效果。
图表示学习与图神经网络
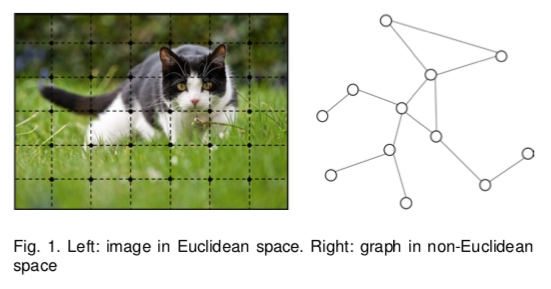
图(Graph),或称为(网络,Network),是一种由对象(节点,node)和关系(连边,edge)构成的数据结构。 Graph Neural Networks: A Review of Methods and Applications 生活中很多数据或系统可以被建模成图,例如社交网络,蛋白质-蛋白质交互网络,疾病传播网络,知识图谱等。图强大到建模和表达能力也吸引了越来越多的学者的关注。与我们熟知的基于格点(2D gird)的图像数据不同,图是非欧数据(non-Euclidean data),为了能够用神经网络进行运算,我们需要先得到节点和连边的一种向量表示,这项技术被称为图表示学习(graph representation learning),或者叫网络嵌入(network embedding),下文不做区分。
受到到自然语言处理中 word2vec Efficient Estimation of Word Representations in Vector Space 的启发,诞生了 DeepWalk Deepwalk: Online learning ofsocialrepresentations、node2vec node2vec: Scalable feature learning for networks、LINE LINE: Large-scale Information Network Embedding 等网络嵌入算法,它们的思路是将节点类比为自然语言中的单词,在图上生成一些经过随机游走(Random Walk)产生的节点序列,把这些序列看成句子。类似于 word2vec 的思想,每个节点都可以用处于其上下文(context)的节点来表示,得到一个长度远小于图上节点数的低维稠密的实值向量。该向量编码了(encode) 图的结构信息,我们可以利用该向量做节点分类、链路预测等下游任务。

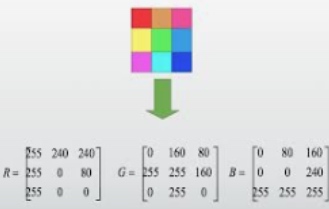
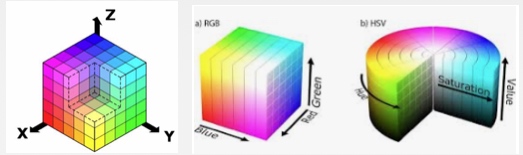
需要注意的是,很多人(尤其是做计算机视觉的人)可能对嵌入这项技术并不熟悉。因为图像天然就是用低维稠密的实值向量来表示的。图像上,每个像素点都对应一个 RGB 值,每个 RGB 通道都是 [0, 255] 的数。此外,颜色空间有多种,比如 RGB、HSV 等,我们会在不同的任务中选取更适合的颜色表示方式。(用 Photoshop 调过照片的朋友可能会更有体会。)
同样的道理,嵌入得到的向量化的节点和连边的表示也是为了图上的下游任务来服务的。而基于随机游走的方法得到的表示信息往往无法针对具体任务进行优化,此外,随机游走算法只能得到图上的结构信息,而无法融合节点的特征信息。因此,研究人员又提出了基于神经网络架构的图表示学习,称为图神经网络 Graph Neural Network (GNN)。感兴趣的朋友可以阅读相关的综述文章。A Gentle Introduction to Graph Neural Network ,Graph Neural Networks: A Review of Methods and Applications,A Comprehensive Survey on Graph Neural Networks。这些算法的基本思路是,针对特定下游任务用端到端 (end-to-end) 的方式进行学习训练,并且可以融合节点的特征信息,比如 cora 引文数据集中,节点的结构信息包含了文章的摘要,这对于做节点分类和链路预测会起到重要作用。我们知道,在 CNN 中,卷积核所定义的是对图像上每个像素点与其周围像素点进行信息交互的方式。同样,GNN中,每个节点也有领域的概念(由图的结构信息所定义),图上的卷积核也是要进行节点和其邻居的信息交互。这里,卷积核的大小往往是固定的,受限于运算复杂度,我们一般使用一阶或者二阶领域。
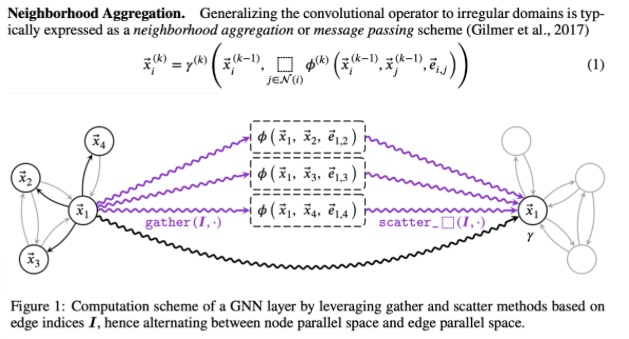
有代表性的 GNN 算法包括,GCN Semi-supervised classification with graph convolutional networks, GAT Graph Attention Networks,GraphSAGE Inductive Representation Learning on Large Graphs。此外,开源社区也出现了一些 GNN 的开发框架,其中,PyTorch Geometric (PyG) 基于 PyTorch 实现,熟悉 PyTorch 的人可以很舒服地使用 PyG 进行 GNN 算法的开发。PyG 提供了一个基础组件,MessagePassing。它认为像 GCN、GAT、GraphSAGE 等算法可以抽象为如图所示的组件。每一层图卷积层要做的就是和相应领域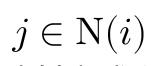 内的节点进行信息的交互。不同的算法的区别在于其所定义的消息的映射方式和领域的选取不用。
内的节点进行信息的交互。不同的算法的区别在于其所定义的消息的映射方式和领域的选取不用。
可变形卷积核
Deformable Convolutional Networks ,这是一篇有趣的文章,我们以往熟知的卷积核是下图左上角所示的那种规则形状的,而这篇文章提出了一种可变形卷积核,它会根据具体的任务和输入数据而改变卷积核的形状,也就是感受野。并且在目标检测任务中取得了比较好的效果。
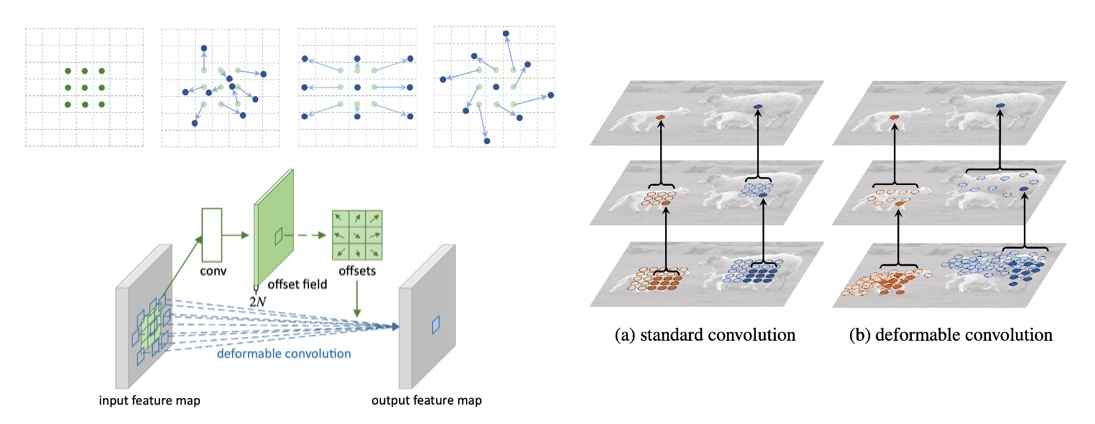
GeniePath 的作者可能是(论文中没有提到)受到了这篇文章的启发,将这个 idea 引入到了 Graph 中。提出了自适应感受野的 GNN 算法。但是该算法的并不是通过调整节点的领域来实现的,而将距离多跳(k-hop)的节点的信息存储在 LSTM 的 memory 中,由神经网络进行学习自动判断哪些信息对于自己完成下游任务是有利的,而进行提取和过滤。
Permutation Invariant
这里提到了一个概念,排列不变性(permutation invariant)。这里[DeepSets: Modeling Permutation Invariance] (https://www.inference.vc/deepsets-modeling-permutation-invariance/) 给出了一个通俗的解释。
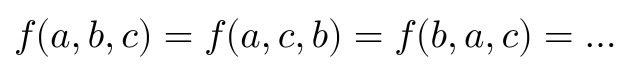 同样的参数输入到函数中,它们的排列顺序并不影响结果。数据结构——集合(set)会用到这样的不变性,相应地,那些在建模中用到集合概念的问题都要遵循排列不变性,例如点云,多主体强化学习,图片场景中多个目标的集合等。在 DeepMind 文章 Graph Matching Networks for Learning the Similarity of Graph Structured Objects 中也有提到排序不变性。"In the past few years graph neural networks (GNNs) have emerged as an effective class of models for learning representations of structured data and for solving various supervised prediction problems on graphs. Such models are invariant to permutations of graph elements by design and compute graph node representations through a propagation process which iteratively aggregates local structural information. These node representations are then used directly for node classification, or pooled into a graph vector for graph classification.
"
本文在算法部分(Proposed Approaches)详细介绍了排列不变性。函数空间要满足图数据所需要的排列不变性。我们要学的是一个函数 f,将图 G 映射到嵌入 H。我们要假设的是该 f 具有排列不变性,学习任务与邻居节点的顺序是无关的。文中用下面公式来定义聚合(aggregator)函数 f 的这个性质,其中 sigma 表示的是任意的排列。
同样的参数输入到函数中,它们的排列顺序并不影响结果。数据结构——集合(set)会用到这样的不变性,相应地,那些在建模中用到集合概念的问题都要遵循排列不变性,例如点云,多主体强化学习,图片场景中多个目标的集合等。在 DeepMind 文章 Graph Matching Networks for Learning the Similarity of Graph Structured Objects 中也有提到排序不变性。"In the past few years graph neural networks (GNNs) have emerged as an effective class of models for learning representations of structured data and for solving various supervised prediction problems on graphs. Such models are invariant to permutations of graph elements by design and compute graph node representations through a propagation process which iteratively aggregates local structural information. These node representations are then used directly for node classification, or pooled into a graph vector for graph classification.
"
本文在算法部分(Proposed Approaches)详细介绍了排列不变性。函数空间要满足图数据所需要的排列不变性。我们要学的是一个函数 f,将图 G 映射到嵌入 H。我们要假设的是该 f 具有排列不变性,学习任务与邻居节点的顺序是无关的。文中用下面公式来定义聚合(aggregator)函数 f 的这个性质,其中 sigma 表示的是任意的排列。
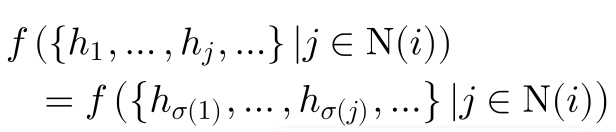
。然后提到了一个定理,当且仅当函数 f 可以被分解为 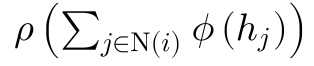 其中 phi 和 rho 是两个映射。那么 f 是具有排列不变形的。并且两个具有排列不变形的函数的复合函数
其中 phi 和 rho 是两个映射。那么 f 是具有排列不变形的。并且两个具有排列不变形的函数的复合函数 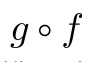 可以等价于 g(f(x))。也是满足排列不变性的,因此,我们可以将函数进行堆叠来设计神经网络。GraphSAGE 提供 LSTM 的聚合器,这种聚合器是不具有 Permutation Invariant 的,因为 LSTM 接收的是遍历节点的隐变量序列,排序是敏感的。此外,这里的 Permutation Invariant 也指图是静态的,不随时间演化。 因为文章中提到 “This is in opposition to temporal graphs.”
可以等价于 g(f(x))。也是满足排列不变性的,因此,我们可以将函数进行堆叠来设计神经网络。GraphSAGE 提供 LSTM 的聚合器,这种聚合器是不具有 Permutation Invariant 的,因为 LSTM 接收的是遍历节点的隐变量序列,排序是敏感的。此外,这里的 Permutation Invariant 也指图是静态的,不随时间演化。 因为文章中提到 “This is in opposition to temporal graphs.”
GeniePath Algorithm
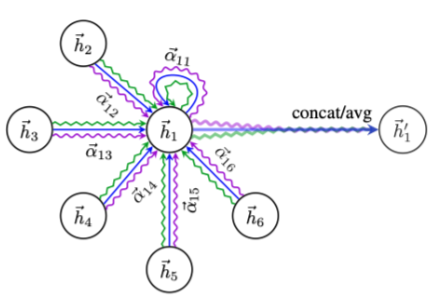
Adaptive Path Layer 是文章的核心内容,相比其他算法中使用事先定义好的路径(pre-defined paths),例如一阶邻居等,Adaptive Path Layer 目标是自学习感受路径,信号在学到的路径上传播。这个问题可以等效于学习每个节点的一个合理的子图,该子图包括两部分,广度方向上给出一阶邻居中节点的权重,深度方向上 t 跳范围内重要的邻居。自适应广度函数定义为  其中 theta 代表参数。H 代表的是节点的嵌入(或者叫隐状态表示)。自适应深度函数定义为,
其中 theta 代表参数。H 代表的是节点的嵌入(或者叫隐状态表示)。自适应深度函数定义为,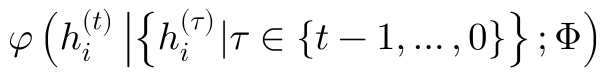
其中,Phi 代表参数。
我们可以将本文和 GAT 或者 GraphSAGE 等常用的非频域的 GNN 框架的区别认为是在它们的基础上加了 memory(通过 LSTM 实现)。存储通过一阶邻域进行的信息传递得到的高阶领域节点的信息。所谓的自适应,自学习,其实就是通过 LSTM 的门对 LSTM 的 memory 所存储的高阶领域信息的提取和过滤 (分别对应遗忘门和输出门)所体现的。而一阶邻域和高阶领域的信息交互体现在 LSTM 的输入门。

注意,广度函数的输出的 H 上标是 tmp,只有将 H_tmp 再输入到深度函数中,才达到一个 epoch 的训练。
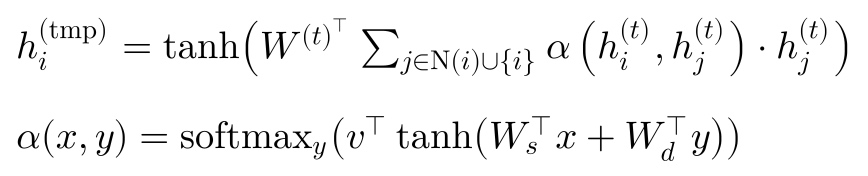
本质来讲,这里是一个去掉了 multi-head 机制的 GAT。
自适应深度函数,本质上就是一个 LSTM,并且这里并没有依赖传统 LSTM 的循环输入,而是只有一次输入。主要利用的是它的存储。其中最重要的公式是最后一个,输出的节点的表示等于存储于 LSTM memory C 的信息和提取和过滤。而提取和过滤的控制是由广度函数的输入决定的。
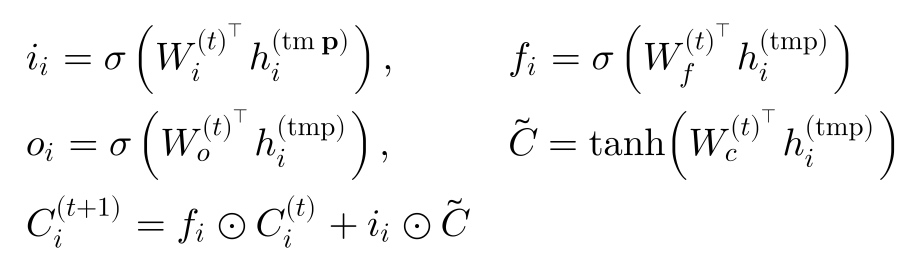
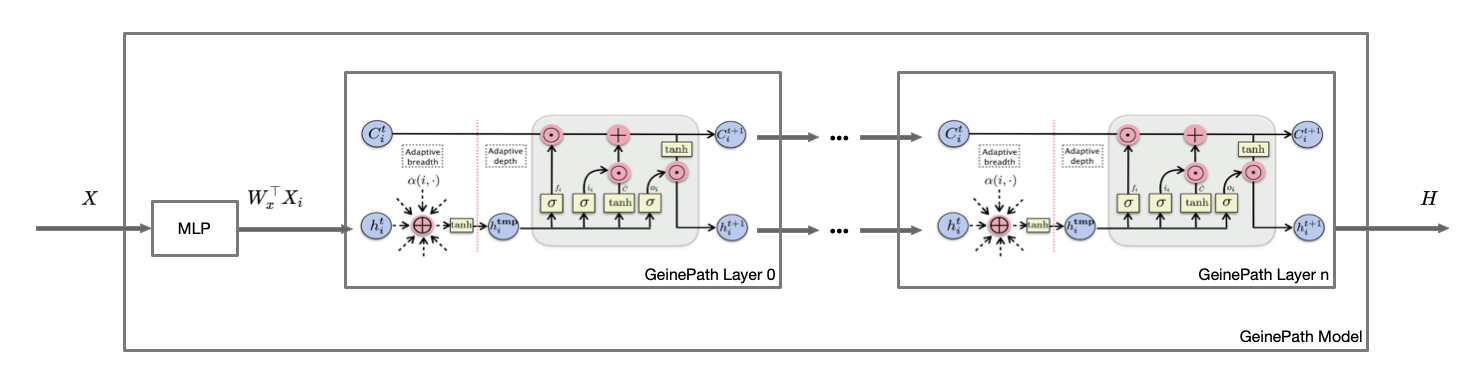
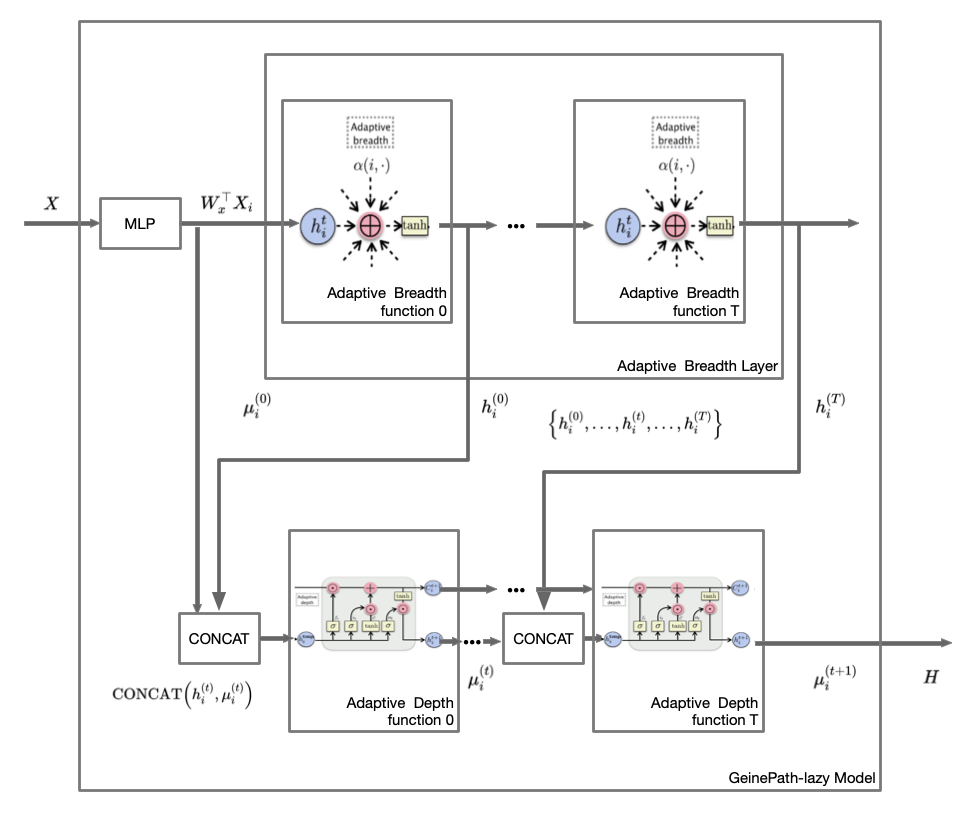
论文仅给出了 Adaptive Path Layer,而没有模型的结构图。这里根据对文章的理解画出神经网络框架。文章提出两个框架,一个是直接将 Adaptive Path Layer 循环 T 次,那么将 t-hop 的节点信息的交互可以融合起来。另一个是 GeniePath-lazy,区别在在于先只过广度函数,得到 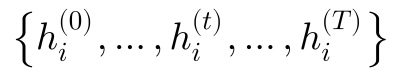 ,再整体输入到深度函数中。
,再整体输入到深度函数中。
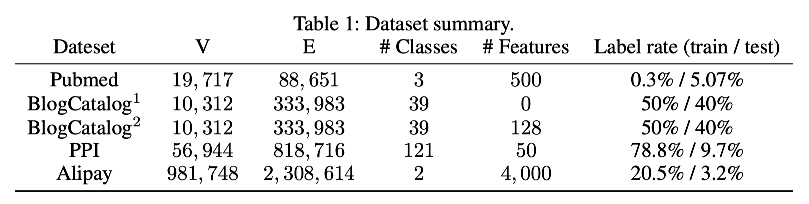
下面列出文中使用的数据信息。
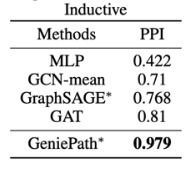
下面是文章给出的实验结果,对比的算法包括 MLP,node2vec,以及几个经典的 GCN 算法。其中 MLP 输入的仅是节点的特征信息,无法利用图结构信息。而 node2vec 输入的仅是图结构信息,无法利用节点的特征信息。

我们能看到 GeniePath 在蛋白质交互网络数据 PPI 上的表现显著强于其他算法,我猜想其中的原因与 PPI 的数据特点有关。在文章 Link Prediction Based on Graph Neural Networks 有这样一段话。“the common neighbor heuristic assumes that two nodes are more likely to connect if they have many common neighbors. This assumption may be correct in social networks, but is shown to fail in protein-protein interaction (PPI) networks --two proteins sharing many common neighbors are actually less likely to interact” ,一般情况下,我们会假设两个节点有更多的共同邻居,它们会倾向于更加相似,但是在蛋白质中,如果两个蛋白质有越多的共同节点,它们更倾向于不发生反应。GeniePath 通过 LSTM 组件融合了图中的高阶邻居信息,使得得到更高的准确率。

GeniePath 的 PyTorch 复现,后续会发到 https://shawnwang.tech https://github.com/shawnwang-tech/GeniePath-pytorch 感兴趣的朋友可以关注。